The peak is the tallest part of the distribution, and the tails are the ends of the distribution.
There are three sorts of kurtosis: mesokurtic, leptokurtic, and platykurtic.

- Mesokurtic: Distributions that are affordable in breadth and curves with a medium peaked peak.
- Leptokurtic: Further values throughout the distribution tails and further values close to the indicate (i.e., sharply peaked with heavy tails)
- Platykurtic: Fewer values throughout the tails and fewer values close to the indicate (i.e., the curve has a flat peak and has additional dispersed scores with lighter tails).
Common kurtosis
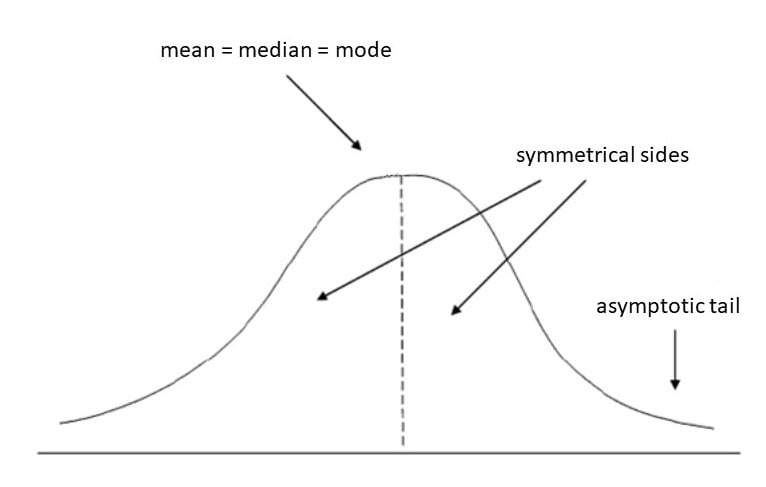
When kurtosis is identical as 3, the distribution is mesokurtic.
This suggests the kurtosis is similar as the traditional distribution; it is mesokurtic (medium peak).
The kurtosis of a mesokurtic distribution is neither extreme nor low; considerably, it is considered to be a baseline for the two totally different classifications.
When kurtosis is zero
When kurtosis is identical as 0, the distribution is platykurtic.
A platykurtic distribution is flatter (a lot much less peaked) as compared with the traditional distribution, with fewer values in its shorter (i.e., lighter and thinner) tails.

Detrimental kurtosis
Detrimental additional values of kurtosis (
A platykurtic distribution is flatter (a lot much less peaked) as compared with the traditional distribution, with fewer values in its shorter (i.e., lighter and thinner) tails.

Constructive kurtosis
Constructive additional values of kurtosis (> 3) level out that distribution is peaked and possesses thick tails. Leptokurtic distributions have constructive kurtosis values.
A leptokurtic distribution has a greater peak (skinny bell) and taller (i.e., fatter and heavy) tails than a standard distribution.

An extreme constructive kurtosis signifies a distribution the place additional of the values are located throughout the tails of the distribution considerably than throughout the indicate.
