Chi-square (χ2) is used to examine hypotheses regarding the distribution of observations into lessons with no inherent score.
What Is a Chi-Sq. Statistic?
The Chi-square examine (pronounced Kai) appears to be on the pattern of observations and may inform us if positive combos of the lessons occur further ceaselessly than we would anticipate by likelihood, given the complete number of situations each class occurred.
It appears to be for an affiliation between the variables. We cannot use a correlation coefficient to seek for the patterns on this info because of the lessons normally do not variety a continuum.
There are three elementary sorts of Chi-square assessments, assessments of goodness of match, the examine of independence, and the examine for homogeneity. All three assessments rely on the similar methodology to compute a examine statistic.
These assessments function by deciphering relationships between observed models of data and theoretical or “anticipated” models of data that align with the null hypothesis.
What’s a Contingency Desk?
Contingency tables (additionally known as two-way tables) are grids whereby Chi-square info is organized and displayed. They provide a elementary picture of the interrelation between two variables and should assist uncover interactions between them.
In contingency tables, one variable and each of its lessons are listed vertically, and the other variable and each of its lessons are listed horizontally.
Furthermore, along with column and row totals, additionally known as “marginal frequencies,” will help facilitate the Chi-square testing course of.
To make sure that the Chi-square examine to be considered dependable, each cell of your anticipated contingency desk might want to have a worth of at least 5.
Each Chi-square examine can have one contingency desk representing observed counts (see Fig. 1) and one contingency desk representing anticipated counts (see Fig. 2).
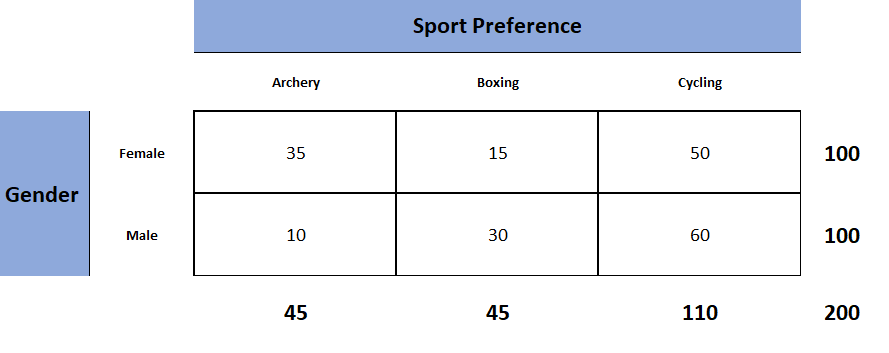
Decide 1. Seen desk (which contains the observed counts).
To amass the anticipated frequencies for any cell in any cross-tabulation whereby the two variables are assumed unbiased, multiply the row and column totals for that cell and divide the product by the complete number of circumstances throughout the desk.

Decide 2. Anticipated desk (what we anticipate the two-way desk to look like if the two categorical variables are unbiased).
To find out if our calculated value for χ2 is important, we moreover should work out the degrees of freedom for our contingency desk using the following methodology: df= (rows – 1) x (columns – 1).
System Calculation

Calculate the chi-square statistic (χ2) by ending the following steps:
- Calculate the anticipated frequencies and the observed frequencies.
- For each observed amount throughout the desk, subtract the corresponding anticipated amount (O — E).
- Sq. the excellence (O —E)².
- Divide the squares obtained for each cell throughout the desk by the anticipated amount for that cell (O – E)² / E.
- Sum the entire values for (O – E)² / E. That’s the chi-square statistic.
- Calculate the degrees of freedom for the contingency desk using the following methodology; df= (rows – 1) x (columns – 1).
As quickly as we have calculated the degrees of freedom (df) and the chi-squared value (χ2), we’ll use the χ2 desk (normally behind a statistics e-book) to check if our value for χ2 is bigger than the important value given throughout the desk. Whether or not it’s, then our end result’s very important on the diploma given.
Interpretation
The chi-square statistic tells you the way in which loads distinction exists between the observed rely in each desk cell to the counts you’d anticipate if there have been no relationship the least bit throughout the inhabitants.
Small Chi-Sq. Statistic: If the chi-square statistic is small and the p-value is large (typically higher than 0.05), this normally signifies that the observed frequencies throughout the sample are close to what might be anticipated beneath the null hypothesis.
The null hypothesis typically states no affiliation between the variables being studied or that the observed distribution matches the anticipated distribution.
In thought, if the observed and anticipated values had been equal (no distinction), then the chi-square statistic might be zero — nonetheless that’s unlikely to happen in precise life.
Huge Chi-Sq. Statistic: If the chi-square statistic is large and the p-value is small (typically decrease than 0.05), then the conclusion is normally that the data does not match the model properly, i.e., the observed and anticipated values are significantly completely completely different. This normally leads to the rejection of the null hypothesis.
Discover ways to Report
To report a chi-square output in an APA-style outcomes half, always rely on the following template:
x2 ( ranges of freedomN = sample dimension ) = chi-square statistic value, p = p value .

Inside the case of the above occasion, the outcomes might be written as follows:
A chi-square examine of independence confirmed that there was a serious affiliation between gender and post-graduation coaching plans, x2 (4, N = 101) = 54.50, p
APA Vogue Tips
- Do not use a zero sooner than a decimal when the statistic cannot be higher than 1 (proportion, correlation, diploma of statistical significance).
- Report exact p values to 2 or three decimals (e.g., p = .006, p = .03).
- However, report p values decrease than .001 as “ p
- Put an space sooner than and after a mathematical operator (e.g., minus, plus, higher than, decrease than, equals sign).
- Do not repeat statistics in every the textual content material and a desk or decide.
p -value Interpretation
You examine whether or not or not a given χ2 is statistically very important by testing it in opposition to a desk of chi-square distributionsconsistent with the number of ranges of freedom to your sample, which is the number of lessons minus 1. The chi-square assumes that you’ve got at least 5 observations per class.
In case you might be using SPSS then you definately’ll have an anticipated p -value.
For a chi-square examine, a p-value that is decrease than or equal to the .05 significance diploma signifies that the observed values are completely completely different to the anticipated values.
Thus, low p-values (p
Take into account that p -values do not level out the probabilities that the null hypothesis is true nonetheless considerably current the probability that one would obtain the sample distribution observed (or a further extreme distribution) if the null hypothesis was true.
A level of confidence essential to simply settle for the null hypothesis can in no way be reached. Attributable to this reality, conclusions ought to choose to each fail to reject the null or accept the selection hypothesis, counting on the calculated p-value.
Using SPSS
The 4 steps beneath current you tips about tips on how to analyze your info using a chi-square goodness-of-fit examine in SPSS (when you’ll have hypothesized that you’ve got equal anticipated proportions).
Step 1: Analyze > Nonparametric Assessments > Legacy Dialogs > Chi-square… on the best menu as confirmed beneath:
Step 2: Switch the variable indicating lessons into the “Verify Variable Guidelines:” subject.
Step 3: Should you want to examine the hypothesis that every one lessons are equally seemingly, click on on “OK.”
Step 4: Specify the anticipated rely for each class by first clicking the “Values” button beneath “Anticipated Values.”
Step 5: Then, throughout the subject to the perfect of “Values,” enter the anticipated rely for sophistication one and click on on the “Add” button. Now enter the anticipated rely for sophistication two and click on on “Add.” Proceed on this way until all anticipated counts have been entered.
Step 6: Then click on on “OK.”
The 4 steps beneath current you tips about tips on how to analyze your info using a chi-square examine of independence in SPSS Statistics.
Step 1: Open the Crosstabs dialog (Analyze > Descriptive Statistics > Crosstabs).
Step 2: Select the variables you want to look at using the chi-square examine. Click on on one variable throughout the left window after which click on on the arrow on the prime to maneuver the variable. Select the row variable and the column variable.
Step 3: Click on on Statistics (a model new pop-up window will appear). Check Chi-square, then click on on Proceed.
Step 4 : (Non-compulsory) Check the sphere for Present clustered bar charts.
Step 5: Click on on OK.
Goodness-of-Match Verify
The Chi-square goodness of match examine is used to examine a randomly collected sample containing a single, categorical variable to an even bigger inhabitants.
This examine is generally used to examine a random sample to the inhabitants from which it was in all probability collected.
The examine begins with the creation of a null and varied hypothesis. On this case, the hypotheses are as follows:
Null Hypothesis (Ho): The null hypothesis (Ho) is that the observed frequencies are the similar (apart from likelihood variation) as a result of the anticipated frequencies. The collected info is per the inhabitants distribution.
Varied Hypothesis (Ha): The collected info simply is not per the inhabitants distribution.
The next step is to create a contingency desk that represents how the data might be distributed if the null hypothesis had been exactly applicable.
The sample’s complete deviation from this theoretical/anticipated info will allow us to draw a conclusion, with a further excessive deviation resulting in smaller p-values.
Verify for Independence
The Chi-square examine for independence appears to be for an affiliation between two categorical variables contained in the similar inhabitants.
Not just like the goodness of match examine, the examine for independence does not look at a single observed variable to a theoretical inhabitants nonetheless considerably two variables inside a sample set to 1 one different.
The hypotheses for a Chi-square examine of independence are as follows:
Null Hypothesis (Ho): There is no such thing as a such factor as a affiliation between the two categorical variables throughout the inhabitants of curiosity.
Varied Hypothesis (Ha): There is no such thing as a such factor as a affiliation between the two categorical variables throughout the inhabitants of curiosity.
The next step is to create a contingency desk of anticipated values that shows how a information set that utterly aligns the null hypothesis would appear.
The very best method to do this is to calculate the marginal frequencies of each row and column; the anticipated frequency of each cell is identical because the marginal frequency of the row and column that corresponds to a given cell throughout the observed contingency desk divided by the complete sample dimension.
Verify for Homogeneity
The Chi-square examine for homogeneity is organized and executed exactly the similar as a result of the examine for independence.
The precept distinction to remember between the two is that the examine for independence appears to be for an affiliation between two categorical variables contained in the similar inhabitants, whereas the examine for homogeneity determines if the distribution of a variable is comparable in each of plenty of populations (thus allocating inhabitants itself as a result of the second categorical variable).
The hypotheses for a Chi-square examine of independence are as follows:
Null Hypothesis (Ho): There is no such thing as a such factor as a distinction throughout the distribution of a categorical variable for plenty of populations or therapies.
Varied Hypothesis (Ha): There is a distinction throughout the distribution of a categorical variable for plenty of populations or therapies.
The excellence between these two assessments typically is a bit troublesome to seek out out, notably throughout the wise features of a Chi-square examine. A reliable rule of thumb is to learn the way the data was collected.
If the data consists of only one random sample with the observations categorised consistent with two categorical variables, it is a examine for independence. If the data consists of a few unbiased random sample, it is a examine for homogeneity.
